Рекомендации по совершенствованию организации и методики преподавания предмета «Математика» в Республике Мордовия на основе выявленных типичных затруднений и ошибок ОГЭ -2022
Анализ результатов выполнения ОГЭ-2022 по математике позволяет представить для учителей-практиков ряд рекомендаций по совершенствованию организации и методики преподавания учебного предмета.
1. Необходимо своевременно изучать нормативно-правовые документы, кодификатор и спецификацию ОГЭ по математике, методические рекомендации ФИПИ на основе типичных затруднений школьников, аналитические и методические материалы, размещенные по адресу
fipi.ru/ege.
2. Необходимо ознакомиться с содержанием КИМ ОГЭ 2023 года. Информация об изменениях в КИМ ОГЭ по математике опубликована 26 августа 2022 года на сайте ФИПИ.
3. В процессе подготовки к новому учебному году необходимо проанализировать результаты ОГЭ по математике 2022 г. в сравнении с результатами прошлых лет, выделить наиболее сложные для изучения темы и типичные ошибки и затруднения обучающихся.
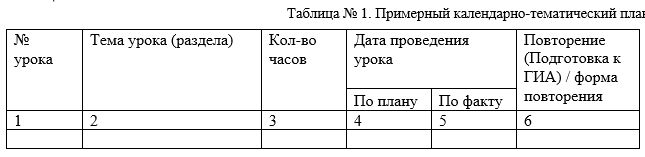
4. Необходимо рационально распределить учебное время, отведенное на изучение тем курса математики 9 класса и подготовку к ОГЭ, с учетом особенностей обучающихся. Поэтому надо провести корректировку календарно-тематического планирования (КТП) с учётом вышеуказанных проблемных тем. Вариант оформления КТП представлен ниже в таблице 1.
5. При подготовке обучающихся к сдаче ГИА-9 по математике целесообразно познакомить их с опубликованными вариантами работ, критериями оценивания заданий. Необходимо также ознакомить обучающихся с обобщённым планом подготовки к итоговой аттестации в предстоящем году. На основе информации, содержащейся в этом документе, следует дать им рекомендации по самостоятельному планированию и повторению учебного материала в течение учебного года. Одним из главных в подготовке обучающихся должен стать принцип активного обучения, когда каждый школьник становится мотивированным субъектом этого процесса.
6. Задача учителя при подготовке к ГИА-9 по математике – не просто подготовить обучающихся к итоговой аттестации, а организовать освоение в полной мере той образовательной программы, которая реализуется в ОО. Основа успешной сдачи ОГЭ по математике – качественное изучение математики, ликвидация пробелов в базовых математических знаниях. Главной задачей подготовки к итоговой аттестации становится планомерная, целенаправленная работа по повторению, систематизации и обобщению изученного материала, по приведению в систему знаний ключевых понятий курса математики. Необходимо учить универсальным приёмам и подходам к решению заданий на основе определений, теорем, правил и алгоритмов, а не тренироваться на одних и тех же заданиях из вариантов КИМ.
7. Параллельно с изучением новых тем курсов алгебры и геометрии в IX классе следует предусмотреть возможность повторения слабо усвоенных тем и разделов. На уроках повторения целесообразно проводить регулярный контроль усвоения знаний на базовом уровне в соответствии с открытым банком тестовых заданий.
8. Важная часть подготовки к ОГЭ – организация учителем чётко спланированной, системы диагностики, использование современных способов проверки знаний, умений и навыков обучающихся и оценочных материалов (в том числе электронных), обеспечивающих в течение всего времени подготовки своевременный и качественный контроль учебных достижений обучающихся, в частности, содержащихся в банке оценочных материалов ФИПИ.
9. В ходе организации итогового повторения и систематизации знаний учащихся в целях подготовки к ГИА, необходимо текущие контрольные задания для учащихся формировать в соответствии с их уровнем математической подготовки и в соответствии со спецификациями контрольных измерительных материалов для проведения ГИА по математике (https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2).
10. Ошибки являются обязательным элементом обучения, полностью избежать ошибок обучающимися невозможно. Поэтому требует внимания изучение информации о типах допускаемых обучающимися ошибок. На уровне ОО необходимо провести анализ ошибок и выработать систему мероприятий по их предупреждению и устранению.
11. Важно в процессе подготовки к сдаче ГИА-9 осуществлять выявление причин математических ошибок, которые возникают у ученика. Это могут быть как причины, связанные с психологическими факторами (в частности, ослабление психических функций: памяти, внимания, мышления), так и причины, обусловленные несовершенством организации учебного процесса (недостаточно ведется подготовительная работа для сознательного усвоения учебного материала, не продумано его целесообразное закрепление в последующем, система упражнений не обеспечивает должной пропедевтической и закрепительной работы, у учащихся не формируются навыки самоконтроля и др.).
12. Для преодоления типичных грубых ошибок у обучающихся учителю следует предусмотреть:
организацию занятий по отработке умений решения задач базового уровня сложности (в форме тренингов, практикумов, зачетов);
включение практико-ориентированных задач в процесс обучения как для решения их на уроках, так и для самостоятельной работы;
включение в дидактические материалы уроков задач из банка задач базового уровня, размещенного на сайте ФИПИ в соответствии с программой обучения курса, начиная с 7 класса;
формирование на уроках и во внеурочной деятельности навыков самоконтроля, навыков устной и письменной математической речи;
решение задач на доказательство, логических задач, задач на делимость чисел, комбинаторных и вероятностных задач, задач из открытого банка заданий для подготовки к ГИА (www.fipi.ru) в соответствии с программой обучения курса, начиная с 7 класса.
13. Среди типичных ошибок, выявляющихся по результатам ОГЭ на протяжении многих лет, традиционно особо выделяются несформированные навыки рационального счета и осмысленного чтения. Отсутствие этих базовых навыков не позволяют выпускникам успешно решать примеры базового уровня сложности, необходимые для получения положительной оценки на экзамене. В связи с этим необходимо проводить систематическую работу в указанных направлениях. В частности, в течение подготовки уделять внимание культуре вычислений (в частности, проведение вычислений без использования калькулятора).
Неверный ответ в задании части 1 зачастую свидетельствует об отсутствии элементарного вычислительного навыка. Напомним, что ответом на задание части 1 является число. Поэтому при вполне осмысленном решении задачи любая вычислительная ошибка приводит к обнулению результата выполняемого задания. Очень часто ученик, знающий, как следует выполнять то или иное задание, не может получить верный ответ только потому, что он допускает ошибку в вычислениях. Учитель математики должен понимать важность и значимость вычислительной культуры и стараться формировать умений рационально вычислять, уделять заданиям на вычисление самое пристальное внимание. Учитель может оттачивать вычислительную культуру учащихся, посредством устного счета, обучающих карточек, математических диктантов, заданий в тестовой форме.
14. Систематизацию знаний обучающихся по алгебре необходимо провести по основным содержательным линиям учебного курса: числовой, линии тождественных преобразований математических выражений, линии уравнений и неравенств, функциональной линии, вероятностно-статистической линии. КИМ-ы ОГЭ проверяют усвоение материала курсов математики 5-6 классов, алгебры 7-9 классов, необходимо систематически повторять соответствующие разделы курса алгебры основной школы.
15. Необходимо отметить, что по-прежнему, остаются недостаточно освоенными выпускниками тождественные преобразования буквенных выражений. Раздел «Тождественные преобразования» (далее ТП) занимает центральное место в школьном курсе математики: изучение ТП имеет самостоятельное значение (связан со следующими вопросами: обобщение операций над числами, проведение вычислений «в общем виде», обучение использованию алгебраической символики; классификация и распознавание алгебраических выражений, преобразование выражений к стандартному виду; рационализация выражений. ТП играют роль вспомогательного «инструмента» при решении уравнений и неравенств, при исследовании функций и ряде других тем школьного курса математики. ТП имеют большое воспитательное значение, т.к. они способствуют развитию у учащихся операционного мышления, воспитанию таких качеств личности, как целеустремленность в поиске решения, сообразительность, аккуратность.
Рекомендуется следующая методика изучения основных групп преобразований: знакомство с его особенностями и характерными чертами; включение каждого нового вида преобразований в целостную систему; знакомство с возможными применениями к решению широкого круга задач.
В результате овладения новым видом преобразований, учащиеся должны: уметь распознавать область применимости изучаемого тождества; знать его формулировку, аналитическую запись, алгоритм применения; уметь проводить преобразование в прямом и обратном порядке; знать о возможных приложениях; уметь использовать в комплексе с другими.
В процессе формирования умения тождественно преобразовывать математические выражения, следует применять специальные методы и приемы обучения: геометрическая иллюстрация преобразований и формул; проговаривание формул вслух или можно поиграть в викторину; один ученик в паре читает левую часть выражения, а второй ученик правую; завести специальную тетрадь-справочник; устраивать диктанты на применение формул; математическое лото и др.
16. Следует особо отметить, что обучающиеся допускают ошибки в решении элементарных уравнений и неравенств, часть выпускников 9-х классов не умеют решать квадратные уравнения и неравенства. А ведь в 10-11 классах практически ежедневно сталкиваются с решением квадратного уравнения. В связи с этим требуется тщательная отработка этой темы.
17. Актуальным остается вопрос формирования у учащихся умений и навыков решения текстовых задач. Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении практико-ориентированных вопросов. Этапы решения задач являются формами развития мыслительной деятельности.
Широко известны серьезные трудности, которые испытывают учащиеся при решении задач. Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д. Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные. Вторая трудность – составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся. Третья трудность – это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.
Ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами. Одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.
18. Необходимо обратить внимание на блок практико-ориентированных заданий № 1-5. Задания проверяют у умения использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели. Решение данных задач использует целый ряд межпредметных связей, развивает вариативность, умение анализировать информацию и делать правильный выбор. Основными трудностями при работе с этими заданиями может являться сложный прикладного характера материал и лимит времени урока. Поэтому необходимо формировать и развивать у обучающихся навык «смыслового чтения». Необходимо научить их выделять ключевые фразы и основные вопросы из текста, разбираться в изображениях рисунков, планов и масштабе фигур на рисунках, анализировать и пользоваться информацией из таблиц. К этому типу задач подготовку нужно начинать с 5 класса. Следует обратить внимание на практико-ориентированные задачи, которые предлагаются ученикам на ВПР. При этом наблюдается постепенное усложнение данных задач при продвижении от класса к классу.
Задания №1-№5. проверяют не только предметные результаты обучения математике, но и метапредметные результаты согласно ФГОС ООО. Перед первым заданием дан рисунок и текст к нему. Все 5 заданий связаны и с рисунком, и с текстом. Темы встречаются разные. Многие уже разобраны и рассмотрены на бескрайних просторах интернета. Но учителю необходимо обязательно следить, что будет предлагаться в открытом банке заданий ОГЭ по математике на сайте ФИПИ (http://oge.fipi.ru/os/xmodules/qprint/index.php?proj).
Многие из предлагаемых задач рассматриваются на канале «Молодой Репетитор» (https://www.youtube.com/watch?v). На предлагаемом канале размещены и другие ролики, посвященные подготовке к ОГЭ. Большая часть задач № 1-№5 из открытого банка с решениями размещены на сайте «Обучающая система Д. Гущина «Решу ОГЭ»» (https://oge.sdamgia.ru/). Обращаем ваше внимание на сайт «Распечатай и реши» (https://www.time4math.ru/oge) Е. А. Ширяевой. Для каждого типа задач на сайте выставлены материалы с пометкой «теория», где автор приводит решение данного типа задачи опираясь на теоретические сведения, которые необходимы для решения всех видов заданий №1-№5. Во втором файле предлагается подборка большого числа заданий по данному типу задачи. Правда ответы ко второму типу файлов автор предлагает платно.
19. Также необходимо обратить внимание на качество изучения геометрического материала. Задания ОГЭ, связанные с применением геометрических знаний, вызывают у школьников определенные затруднения. Изучение геометрического материала предполагает правильное оформление задачи (выполнение правильного и рационального чертежа), поиск логически обоснованного решения, основанного на знании геометрических фактов – все это приводит к значительным временным затратам (подчас за один урок решается только одна-две задачи). Учитывая данную специфику геометрии, для успешного освоения геометрического материала можно порекомендовать учителям включать в урок устные задачи по геометрии, задачи по готовым чертежам, активно использовать печатные тетради с обучающими заданиями.
20. Важно обратить внимание на основной список тем по геометрии, подлежащий контролю в конце 9 класса на уроках планиметрии: виды треугольников; замечательные линии и точки в треугольнике (медиана, средняя линия, высота, биссектриса, серединный перпендикуляр к стороне); вписанная и описанная окружности; тригонометрические функции острого угла прямоугольного треугольника; теорема Пифагора; теоремы синусов и косинусов; виды четырехугольников; свойства и признаки параллелограмма, прямоугольника, ромба, квадрата, трапеции; формулы площадей плоских фигур; координатный и векторный методы решения задач. Прежде всего незнание фундаментальных метрических формул и неумение их использовать, а также незнание свойств основных планиметрических фигур полностью лишает учащихся возможности применять свои знания по планиметрии при решении соответствующих задач.
21. Обратить внимание на формирование умения доказывать утверждения. Умение доказывать формируется постепенно не только в процессе решения задач, но и при доказательстве теорем, это одна из самых важных составляющих геометрии. Поэтому учителю нельзя игнорировать из-за нехватки времени представление доказательства на уроках самому и опрос учащихся по доказательству теорем; требовать от учащихся пояснений и доказательств утверждений при решении задач, обоснованных устных ответов, обучать доказательству.
22. Включение заданий вероятностно-статистической линии в КИМы государственной (итоговой) аттестации за курс математики в 9 классе делает необходимым регулярное изучение данного раздела. Рекомендуем в процессе подготовки обратить внимание на повторение ряда тем следующим образом: 1) статистические характеристики; сбор и группировка статистических данных; наглядное представление статистической информации (представление данных в виде таблиц, диаграмм, графиков); 2) множество (элемент множества, подмножество, диаграммы Эйлера); операции над множествами; комбинаторика (перебор вариантов; правило суммы, умножения, решение комбинаторных задач путем систематического перебора возможных вариантов, а также с использованием правил суммы и умножения); 3) комбинаторные задачи; перестановки, размещения, сочетания; вероятность случайных событий (вычисление частоты события с использованием собственных наблюдений и готовых статистических данных); нахождение вероятности случайных событий в простейших случаях.
23. Описание конкретных технологий подготовки обучающихся к ОГЭ по математике, приемы работы учителей практиков можно найти в ряде публикаций:
cyberleninka.ru/article/n/formirovanie-predmetnoy-gotovnosti-uchaschihsya-k-ege-po-matematike
урок.рф/library/effektivnie_priemi_i_metodi_podgotovki_uchashihsya_k_144002.html
file:///C:/Users/User/Downloads/gotovimsya-k-edinomu-gosudarstvennomu-ekzamenu-po-matematike.pdf
file:///C:/Users/User/Downloads/nekotorye-metodicheskie-aspekty-podgotovki-shkolnikov-k-ege-po-matematike.pdf
24. Для эффективной подготовки к экзаменам целесообразно использовать только официальные ресурсы: официальный сайт Рособрнадзора – obrnadzor.gov.ru/gia/ и сайт ФИПИ – fipi.ru/. На этих сайтах размещаются актуальные сведения, охватывающие все особенности ОГЭ по математике.
25. Целью открытых банков ФИПИ является предоставление обучающимся возможности потренироваться в решении заданий, подобных тем, которые могут встретиться на экзаменах. Задания из открытых банков могут быть использованы как в рамках школьных уроков, так и при самостоятельной подготовке к ГИА.
26. На практике учителю математики представляется целесообразным использовать различные интернет-ресурсы, в частности:
Информационный портал ОГЭ (https://obrnadzor.gov.ru/gia/gia-11/ ). На портале представлена вся официальная информация об экзаменах. Расписание, документы, демонстрационные задания, общественное наблюдение.
Сдам ОГЭ / Решу ЕГЭ (https://ege.sdamgia.ru/ ) – сайт Д. Д. Гущина. На сайте можно не только решать тесты, но и задавать вопросы, на которые регулярно отвечают администраторы портала. В разделе «Каталог заданий» собрано большое количество тематических задач: можно выбрать определённую тему и решать десятки типовых заданий, чтобы её отработать или составить свой собственный тест.
Foxford.ru (foxford.ru ). На сайте ученикам предлагается пройти обучение по программам от 3 до 11 класса, они могут всесторонне подготовиться к сдаче ОГЭ, а их родители – посетить занятия и узнать о развитии детей. У Фоксфорд есть школа на дому с персональными учителями. В отличие от обычного экстерната в Фоксфорде с ребенком будут работать преподаватели из известных ВУЗов России, а также члены жюри олимпиад и эксперты ЕГЭ/ОГЭ.
Яндекс.ЕГЭ (ege.yandex.ru ). На сервисе Яндекса представлена большая база тестов ОГЭ. На сайте можно пройти тестирование, сделать задания по определенным темам разных уровней сложности, а также ознакомиться с тщательным разбором заданий ОГЭ по математике. Кроме самих тестов, на сайте есть раздел с видеолекциями (вебинарами) с разборами заданий от опытных преподавателей.
27. Большое значение в решении поставленных задач имеет плодотворная работа муниципальных методических объединений учителей математики. Задача методических объединений – оказывать помощь учителям по следующим направлениям:
— развитие творческой инициативы учителя математики посредством участия в различных профессиональных конкурсах;
— регулярное посещение учителями-наставниками уроков математики молодых (малоопытных) учителей математики (возможна организация непрерывно действующих семинаров по обмену опытом);
— организация семинаров-практикумов для учителей по анализу демонстрационного варианта ОГЭ с использованием материалов открытого банка заданий, опубликованного на официальном сайте ФИПИ, для подготовки, как учителей, так и школьников к решению задач новой перспективной модели ОГЭ;
— вовлечение учащихся с целью развития творческих способностей в различные математические конкурсы, проекты, олимпиады.
В августе – сентябре 2022 г. на заседаниях школьных / городских / муниципальных методических объединений обсудить результаты ОГЭ-2022 по математике.
Учитывая выявленные типичные затруднения и ошибки выпускников 9 классов 2022 г., ГБУ ДПО РМ «ЦНППМ «Педагог13.ру» необходимо продолжить системную работу по совершенствованию процесса преподавания математики в Республике Мордовия и улучшению подготовки учащихся по предмету. В связи с этим рекомендуется:
1. Обсудить в сентябре 2022 г. результаты ОГЭ-2022 по математике.
2. Рекомендовать учителям математики обучение на курсах повышения квалификации на базе ГБУ ДПО РМ «ЦНППМ «Педагог13.ру» по дополнительным профессиональным программам повышения квалификации: «Алгебраические задания ЕГЭ: практический курс по решению и технологии обучения» (36 часов), «Геометрические задания ЕГЭ: практический курс по решению и технологии обучения» (36 часов).
3. Обеспечить консультирование и тьюторское сопровождение педагогов через созданный на базе ГБУ ДПО РМ «ЦНППМ «Педагог 13.ру» консультационный центр.
4. Организовать в рамках деятельности лаборатории математического образования и информатики обучающие семинары и вебинары и другие образовательные события по совершенствованию методических компетенций учителей в области подготовки обучающихся к участию в ГИА, по диссеминации инновационного педагогического опыта.
5. Продолжить работу по консультированию педагогов, в том числе адресному (на основе анализа результатов ОГЭ-2022 года), для школ с низкими результатами обучения и школ, функционирующих в неблагоприятных социальных условиях, в Республике Мордовия («500+») в течение 2022 – 2023 учебного года.
6. Использовать возможности электронного образовательного ресурса «Региональная электронная школа «На 5+» для подготовки обучающихся к государственной итоговой аттестации dio.edurm.ru/course/index.php?categoryid=12
7. Организовать анонсирование и участие педагогов в образовательных событиях по вопросам подготовки к государственной итоговой аттестации, используя ресурсы сетевого профессионального сообщества учителей математики «Педагог 13.ру» socpedagog13.edurm.ru/groups/18